Data Network Research--3 Dimension Poisson Point Process Connection
In the class Data Network, professor Neely taught about the Poisson Point Process in 2 Dimension. How to analyze data connection probability if different data access points pop according to Poisson Process in 2 dimensions. However, I was thinking about how to extend this scenario into 3 dimensions during the class. I thought this would be an interesting topic to do research on. Since it would involve different scenarios and it would be closer to real-world problems.
I Introduction
λ = points/volume is the random placement of point;
Suppose v = 1, we split the whole space into C subspaces with volume 1/𝐶. Let 𝑁 , … , 𝑁 be
the random number of points in the subspace. Then the probability of k users in cell i is:
II Simulation
Basic Algorithm:
- Generate a Poisson random number to be the total number of the PPP points in the cube.
- Independently generate n points (xi, yi), that are uniformly distributed in this cube.
- Choose a positive integer as the constant a, and another integer as the cell number which is supposed to be multiple of 27, also we got the edge s of cell.
- Traverse the whole three arrays in the step of 3s and find the empty cell, mark them.
- Check out the connectivity of the cube.
The simulation example: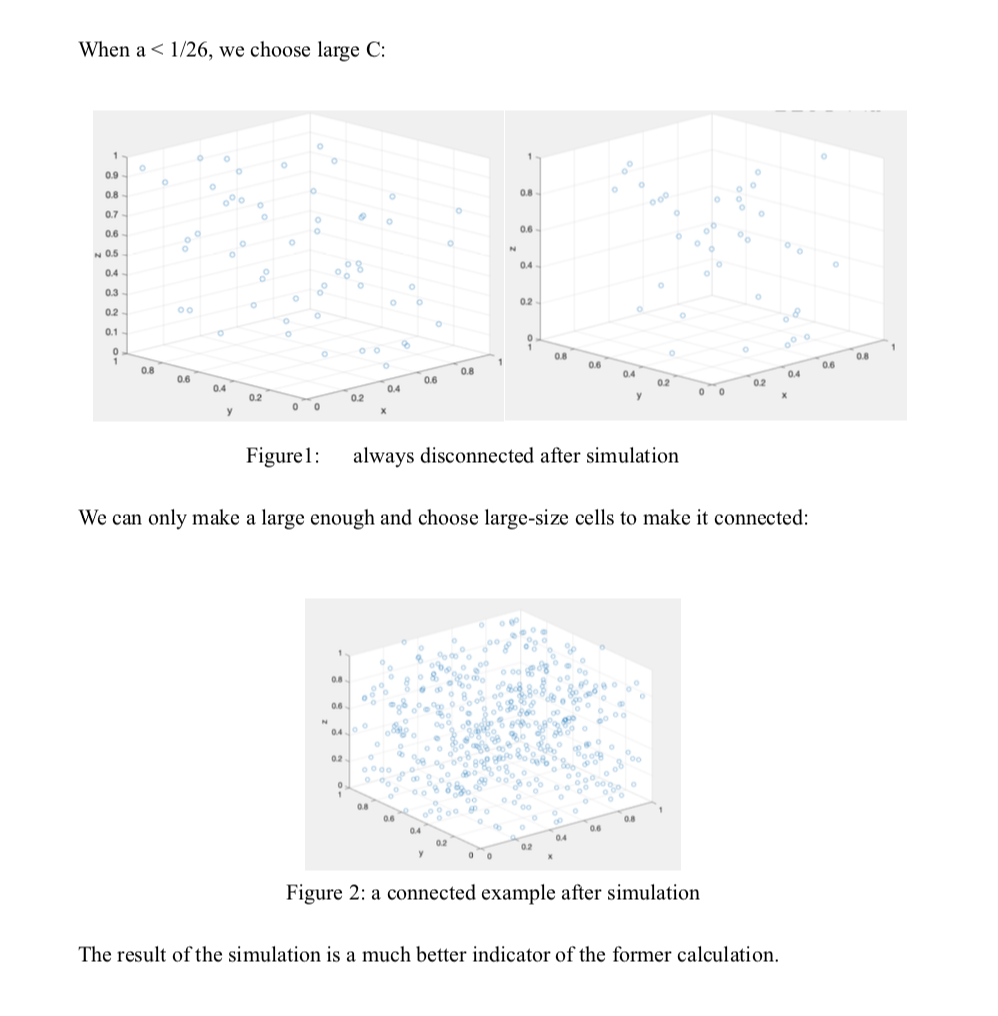
III 3D PPP in Sphere Space
First, do a quick analysis of how to get the probability, that a point can connect to the outside with an r radius sphere radiation range. Recall that it still focuses on a Poisson Point Process.
To begin with, define N(A), which is a Poisson process with intensity of λ>0 so that it leads to the equation





